
Mathematical Economics
Economic inequality, defined as the uneven distribution of income or wealth among a population, is a complex issue that affects societal structure, access to resources, and individual well-being. Researchers, policymakers, and economists often turn to mathematical models to understand, quantify, and compare inequality levels across regions or time periods. Among the most widely used tools are the Lorenz Curve and Gini Coefficient, both of which offer valuable insights into income distribution.
This article explores these mathematical models in detail. We’ll examine the construction and interpretation of Lorenz curves, the calculation and significance of the Gini coefficient, and real-world applications of these models in measuring economic inequality.
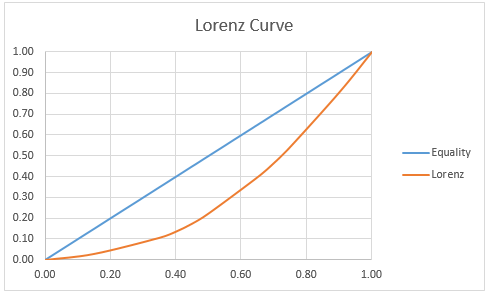
Lorenz Curve vs. Inequality
Introduction to Economic Inequality
Economic inequality is a multi-dimensional issue influenced by various social, political, and economic factors. In a purely egalitarian society, resources would be distributed equally among all individuals, but in reality, factors such as education, family background, and regional disparities contribute to unequal distributions of wealth and income.
To study and quantify this inequality, mathematical models allow researchers to create visualizations and statistics that capture the degree of disparity within a population. These models help policymakers understand where intervention may be needed and allow for comparison across countries or over time.
Understanding the Lorenz Curve
The Lorenz Curve is a graphical representation of income or wealth distribution within a population. It was introduced by economist Max O. Lorenz in 1905 and has since become a standard tool in economics for visualizing inequality.
The Lorenz Curve plots the cumulative percentage of total income or wealth on the vertical axis against the cumulative percentage of the population on the horizontal axis. If income were distributed perfectly equally, every percentage of the population would correspond to the same percentage of total income, resulting in a 45-degree line known as the line of equality. The further the Lorenz Curve is from this line, the greater the level of inequality.
Constructing the Lorenz Curve
Constructing a Lorenz Curve involves the following steps:
- Sort the Population by Income: Arrange individuals or households in ascending order of income or wealth.
- Calculate Cumulative Percentages: For each segment of the population, calculate the cumulative percentage of income received and the cumulative percentage of the population.
- Plot the Lorenz Curve: Plot the cumulative population percentages on the horizontal axis and the cumulative income or wealth percentages on the vertical axis.
Example Calculation
Consider a simplified economy with five individuals, each with a different level of income. We’ll assume the following incomes: $10, $20, $30, $40, and $100.
- Sort the Income Data: The data is already in ascending order.
- Calculate Cumulative Percentages:
- Population percentages: 20%, 40%, 60%, 80%, 100%
- Cumulative income: $10, $30, $60, $100, $200
- Income percentages: 5%, 15%, 30%, 50%, 100%
- Plotting the Points:
- Point 1: (20%, 5%)
- Point 2: (40%, 15%)
- Point 3: (60%, 30%)
- Point 4: (80%, 50%)
- Point 5: (100%, 100%)
These points form the Lorenz Curve for this population, which can then be graphed to visualize the inequality in income distribution.
Interpreting Lorenz Curves
A Lorenz Curve that is closer to the line of equality represents a more equal income distribution. As the Lorenz Curve bows further from the line, inequality increases. The shape and position of the Lorenz Curve can reveal:
- Degree of Inequality: A larger area between the Lorenz Curve and the line of equality indicates higher inequality.
- Poverty Concentration: When the Lorenz Curve bows steeply near the origin, it suggests that a small percentage of the population controls a large portion of the income or wealth.
Lorenz Curves provide a visual way to assess income distribution; however, for precise quantification, the Gini Coefficient is often used.
The Gini Coefficient: Measuring Inequality
The Gini Coefficient is a scalar measure derived from the Lorenz Curve, representing the level of inequality within a distribution. Developed by Italian statistician Corrado Gini, the Gini Coefficient is calculated as the ratio of the area between the Lorenz Curve and the line of equality to the total area under the line of equality.
Calculating the Gini Coefficient
The Gini Coefficient (\(G\)) can be calculated using the following formula:
\[G = \frac{A}{A + B}\]where:
- A is the area between the line of equality and the Lorenz Curve.
- B is the area under the Lorenz Curve.
Alternatively, if income data is available for every individual, the Gini Coefficient can be calculated using this formula:
\[G = 1 - \sum_{i=1}^{n} (X_i - X_{i-1}) (Y_i + Y_{i-1})\]where \(X_i\) and \(Y_i\) represent cumulative percentages of the population and income, respectively.
Example Calculation of the Gini Coefficient
Using the Lorenz Curve data from our earlier example:
- Compute the area between the Lorenz Curve and the line of equality (Area A).
- Sum the area beneath the Lorenz Curve (Area B).
- Calculate G using the formula.
A lower Gini Coefficient indicates a more equal distribution, while a higher coefficient suggests greater inequality.
Interpretation of Gini Values
The Gini Coefficient ranges from 0 to 1:
- 0 indicates perfect equality, where everyone has an equal share of income or wealth.
- 1 denotes perfect inequality, where all income is held by a single individual or household.
Real-world Gini Coefficients typically fall between 0.2 and 0.6. For example, Scandinavian countries with strong social welfare systems often have Gini Coefficients below 0.3, while countries with higher inequality levels, such as South Africa or Brazil, have coefficients above 0.5.
Advantages and Limitations of Lorenz Curves and Gini Coefficients
Advantages
- Intuitive Visualization: Lorenz Curves provide a clear visual representation of inequality.
- Quantitative Measure: The Gini Coefficient offers a precise, single-value summary of income or wealth distribution.
- Comparative Power: Both tools facilitate cross-country and historical comparisons of inequality levels.
Limitations
- Ignores Distribution Details: The Gini Coefficient does not reveal where inequality exists within the distribution.
- Sensitivity to Population Changes: Both measures can be affected by changes in population size and structure.
- Limited Policy Insight: While these tools highlight inequality levels, they do not suggest causes or remedies for inequality.
Real-World Applications and Examples
-
Country Comparisons: Governments and international organizations, such as the World Bank, use Gini Coefficients to compare inequality levels across countries. For example, Scandinavian countries have relatively low Gini values, while countries in Latin America and sub-Saharan Africa tend to have higher values.
-
Income and Wealth Studies: Economists use Lorenz Curves and Gini Coefficients to study income and wealth distribution within a single country. By comparing values over time, they can track changes in inequality and assess the impact of economic policies.
-
Public Policy and Social Welfare: Policymakers use these models to evaluate the effectiveness of social welfare programs and tax policies aimed at reducing inequality. For instance, progressive taxation is intended to narrow the gap between high-income and low-income earners, thus lowering the Gini Coefficient.
Critiques and Alternative Measures of Inequality
While Lorenz Curves and Gini Coefficients are widely used, they have limitations and are not universally accepted as the best measures of inequality. Some alternative models include:
- Theil Index: Measures inequality based on entropy and is sensitive to differences within income groups.
- Atkinson Index: Focuses on the degree of inequality that society deems unacceptable, allowing for customization based on social welfare preferences.
- Palma Ratio: Compares the share of income held by the top 10% of earners with that held by the bottom 40%, providing an intuitive view of extreme inequality.
The Role of Mathematical Models in Understanding Inequality
Lorenz Curves and Gini Coefficients are essential tools for economists and policymakers studying inequality. These models offer insights into income distribution patterns and allow for meaningful comparisons across regions and time periods. However, to fully understand and address economic inequality, it is essential to complement these tools with additional analysis, data, and policy evaluation.
In combination with other measures, Lorenz Curves and Gini Coefficients enable a comprehensive assessment of inequality, guiding policies that aim to create fairer and more equitable societies.
Appendix: Python Code Examples for Lorenz Curve and Gini Coefficient
import numpy as np
import matplotlib.pyplot as plt
# Lorenz Curve Calculation
def lorenz_curve(data):
sorted_data = np.sort(data)
cumulative_data = np.cumsum(sorted_data) / np.sum(sorted_data)
cumulative_data = np.insert(cumulative_data, 0, 0)
return cumulative_data
# Plotting Lorenz Curve
def plot_lorenz_curve(data):
lorenz = lorenz_curve(data)
plt.plot(np.linspace(0, 1, len(lorenz)), lorenz, label="Lorenz Curve")
plt.plot([0, 1], [0, 1], linestyle="--", label="Line of Equality")
plt.xlabel("Cumulative Population")
plt.ylabel("Cumulative Income")
plt.legend()
plt.show()
# Gini Coefficient Calculation
def gini_coefficient(data):
sorted_data = np.sort(data)
n = len(data)
cumulative_sum = np.cumsum(sorted_data)
relative_mean_difference = np.sum((2 * np.arange(1, n + 1) - n - 1) * sorted_data)
return relative_mean_difference / (n * cumulative_sum[-1])
# Example Data
income_data = [10, 20, 30, 40, 100]
# Calculate and Print Lorenz Curve
lorenz_data = lorenz_curve(income_data)
print("Lorenz Curve Data:", lorenz_data)
# Plot Lorenz Curve
plot_lorenz_curve(income_data)
# Calculate and Print Gini Coefficient
gini = gini_coefficient(income_data)
print("Gini Coefficient:", gini)
Appendix: Java Code Examples for Lorenz Curve and Gini Coefficient
import java.util.Arrays;
public class InequalityMetrics {
// Calculate Lorenz Curve Data
public static double[] lorenzCurve(double[] data) {
Arrays.sort(data);
double sum = Arrays.stream(data).sum();
double[] cumulativeData = new double[data.length + 1];
cumulativeData[0] = 0.0;
for (int i = 0; i < data.length; i++) {
cumulativeData[i + 1] = cumulativeData[i] + data[i] / sum;
}
return cumulativeData;
}
// Calculate Gini Coefficient
public static double giniCoefficient(double[] data) {
Arrays.sort(data);
int n = data.length;
double cumulativeSum = 0.0;
double relativeMeanDifference = 0.0;
for (int i = 0; i < n; i++) {
cumulativeSum += data[i];
relativeMeanDifference += (2 * (i + 1) - n - 1) * data[i];
}
return relativeMeanDifference / (n * cumulativeSum);
}
// Example Usage
public static void main(String[] args) {
double[] incomeData = {10, 20, 30, 40, 100};
// Calculate Lorenz Curve
double[] lorenzData = lorenzCurve(incomeData);
System.out.println("Lorenz Curve Data: " + Arrays.toString(lorenzData));
// Calculate Gini Coefficient
double gini = giniCoefficient(incomeData);
System.out.println("Gini Coefficient: " + gini);
}
}
Appendix: JavaScript Code Examples for Lorenz Curve and Gini Coefficient
// Calculate Lorenz Curve Data
function lorenzCurve(data) {
data.sort((a, b) => a - b);
const sum = data.reduce((acc, val) => acc + val, 0);
let cumulativeData = [0];
data.reduce((cumulativeSum, value) => {
cumulativeSum += value;
cumulativeData.push(cumulativeSum / sum);
return cumulativeSum;
}, 0);
return cumulativeData;
}
// Calculate Gini Coefficient
function giniCoefficient(data) {
data.sort((a, b) => a - b);
const n = data.length;
const cumulativeSum = data.reduce((acc, val) => acc + val, 0);
let relativeMeanDifference = 0;
for (let i = 0; i < n; i++) {
relativeMeanDifference += (2 * (i + 1) - n - 1) * data[i];
}
return relativeMeanDifference / (n * cumulativeSum);
}
// Example Usage
const incomeData = [10, 20, 30, 40, 100];
// Calculate Lorenz Curve
const lorenzData = lorenzCurve(incomeData);
console.log("Lorenz Curve Data:", lorenzData);
// Calculate Gini Coefficient
const gini = giniCoefficient(incomeData);
console.log("Gini Coefficient:", gini);



