Introduction
What is the Probability Integral Transform?
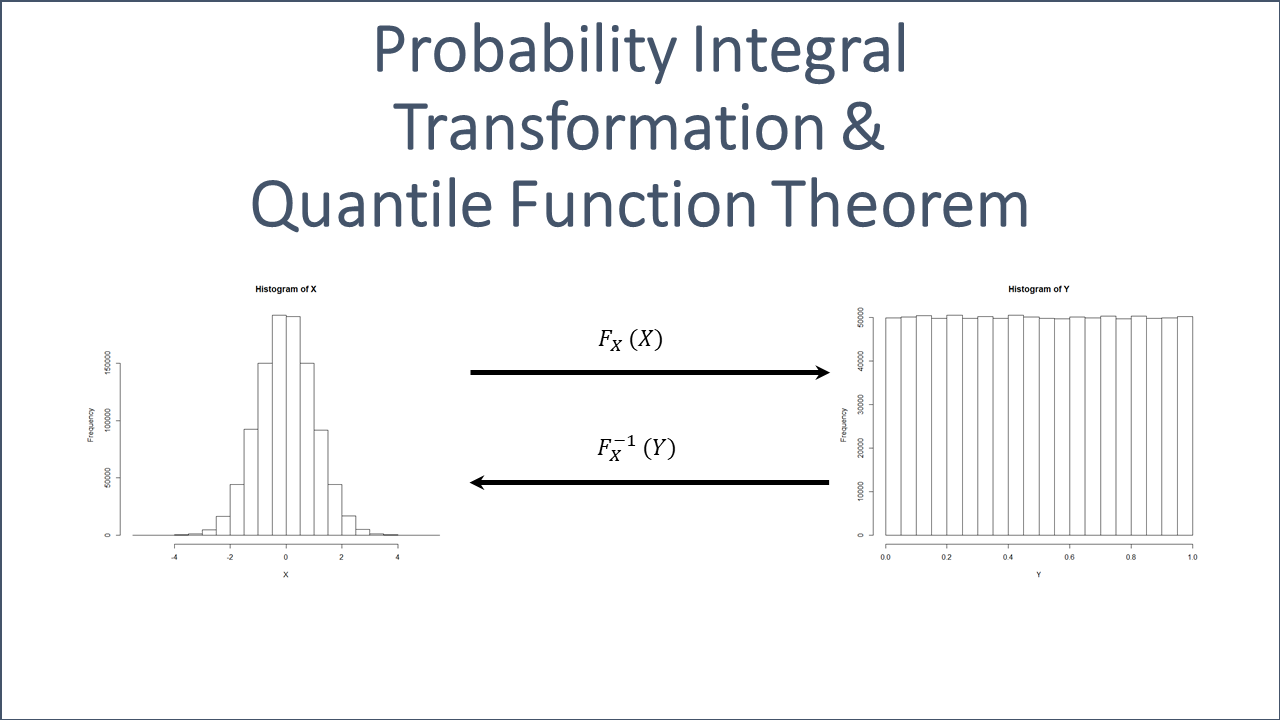
The Probability Integral Transform is a fundamental concept in statistics and probability theory. It enables the conversion of a random variable with any continuous distribution into a random variable with a uniform distribution on the interval \([0, 1]\).
Definition and Basic Explanation
Given a continuous random variable \(X\) with a cumulative distribution function (CDF) \(F_X(x)\), the transform states that the random variable \(Y = F_X(X)\) follows a uniform distribution on the interval \([0, 1]\). This can be expressed mathematically as:
\[Y = F_X(X)\]where:
- \(X\) is a continuous random variable.
- \(F_X(x)\) is the CDF of \(X\).
- \(Y\) is a new random variable that is uniformly distributed over \([0, 1]\).
To understand why this transformation works, consider the properties of the CDF. The CDF, \(F_X(x)\), of a random variable \(X\) is defined as:
\[F_X(x) = P(X \leq x)\]This function \(F_X(x)\) maps values of \(X\) to probabilities in the range \([0, 1]\). Since \(F_X(x)\) is a monotonically increasing function that spans from 0 to 1 as \(x\) goes from \(-\infty\) to \(\infty\), applying \(F_X\) to \(X\) standardizes these probabilities, transforming \(X\) into a new random variable \(Y\) that is uniformly distributed between 0 and 1.
Importance in Statistics and Probability Theory
The Probability Integral Transform is crucial for several reasons:
-
Simplification and Standardization: By transforming any continuous random variable into a uniform distribution, it simplifies the process of working with different distributions. This standardization is particularly useful in theoretical derivations and practical applications.
-
Foundation for Further Analysis: Many statistical methods and tests rely on the uniformity of transformed data. For example, goodness of fit tests often use the Probability Integral Transform to compare observed data with expected distributions.
-
Enabling Complex Models: The transform is a key tool in constructing copulas, which are functions used to describe the dependence structure between random variables. This is particularly useful in multivariate analysis where understanding the relationship between variables is crucial.
-
Improving Simulation and Random Sampling: In Monte Carlo simulations and random sample generation, the Probability Integral Transform allows for the creation of samples from any desired distribution. By first generating uniform random variables and then applying the inverse CDF of the target distribution, we can simulate data that follows complex distributions.
Understanding the Probability Integral Transform provides a powerful toolset for both theoretical explorations and practical applications in statistics and probability. It serves as a bridge between various distributions, facilitating analysis, testing, and simulation in a standardized manner.
Why Does It Work?
The Probability Integral Transform works due to the inherent properties of cumulative distribution functions (CDFs). The transformation of any continuous random variable into a uniformly distributed random variable relies on the mathematical basis and behavior of CDFs.
Explanation of the Mathematical Basis
To understand why the Probability Integral Transform works, let’s start with the definition of a cumulative distribution function (CDF). For a continuous random variable %%X\(with CDF\)F_X(x)$$, the CDF is defined as:
\[F_X(x) = P(X \leq x)\]This equation states that \(F_X(x)\) is the probability that the random variable \(X\) takes on a value less than or equal to \(x\).
Now, consider the transformed variable \(Y\):
\[Y = F_X(X)\]Here, \(Y\) is a new random variable created by applying the CDF of \(X\) to itself. To show that \(Y\) is uniformly distributed over the interval \([0, 1]\), we need to demonstrate that the CDF of \(Y\), denoted as \(F_Y(y)\), follows a uniform distribution.
The CDF of \(Y\) is given by:
\[F_Y(y) = P(Y \leq y) = P(F_X(X) \leq y)\]Since \(F_X\) is a monotonically increasing function, we can invert it to find \(X\):
\[P(F_X(X) \leq y) = P(X \leq F_X^{-1}(y))\]By the definition of the CDF \(F_X\), we have:
\[P(X \leq F_X^{-1}(y)) = F_X(F_X^{-1}(y)) = y\]Therefore:
\[F_Y(y) = y\]This shows that the CDF of \(Y\) is \(y\) for \(y\) in the interval \([0, 1]\), which is the CDF of a uniform distribution on \([0, 1]\). Thus, \(Y\) is uniformly distributed.
Role of Cumulative Distribution Functions (CDFs)
The role of CDFs is central to the Probability Integral Transform. The CDF \(F_X(x)\) encapsulates all the probabilistic information about the random variable \(X\). When we apply \(F_X\) to \(X\), we leverage this information to standardize the variable into a uniform distribution.
Key properties of CDFs that make the Probability Integral Transform work include:
-
Monotonicity: CDFs are monotonically increasing functions. This means that as the value of \(X\) increases, \(F_X(x)\) also increases. This property ensures that the transformation \(Y = F_X(X)\) is well-defined and maps \(X\) to the interval \([0, 1]\).
-
Range: The range of a CDF is always between 0 and 1, inclusive. This range matches the desired uniform distribution range for the transformed variable \(Y\).
-
Invertibility: For continuous random variables, the CDF \(F_X\) is invertible. This allows us to map back from the uniform distribution to the original distribution if needed, using the inverse CDF \(F_X^{-1}\).
-
Probabilistic Interpretation: The CDF \(F_X(x)\) gives the probability that \(X\) is less than or equal to \(x\). This probabilistic interpretation is preserved in the transform, making \(Y = F_X(X)\) a probabilistically meaningful transformation.
The Probability Integral Transform leverages these properties of CDFs to convert any continuous random variable into a uniformly distributed variable, facilitating various statistical methods and analyses.
author_profile: false categories:
- Statistics classes: wide date: ‘2024-05-21’ excerpt: An in-depth guide to understanding and applying the Probability Integral Transform in various fields, from finance to statistics. header: image: /assets/images/data_science_2.jpg og_image: /assets/images/data_science_3.jpg overlay_image: /assets/images/data_science_2.jpg show_overlay_excerpt: false teaser: /assets/images/data_science_2.jpg twitter_image: /assets/images/data_science_3.jpg keywords:
- Probability integral transform
- Cumulative distribution function
- Goodness of fit
- Copula construction
- Financial risk management
- Monte carlo simulations
- Hypothesis testing
- Credit risk modeling
- R
- Mathematics
- Statistics
- Data science
- Machine learning seo_description: A comprehensive exploration of the probability integral transform, its theoretical foundations, and practical applications in fields such as risk management and marketing mix modeling. seo_title: ‘Probability Integral Transform: Theory and Applications’ seo_type: article summary: This article explains the Probability Integral Transform, its role in statistical modeling, and how it is applied in diverse fields like risk management, hypothesis testing, and Monte Carlo simulations. tags:
- Probability integral transform
- Cumulative distribution function
- Uniform distribution
- Copula construction
- Goodness of fit
- Monte carlo simulations
- Hypothesis testing
- Marketing mix modeling
- Credit risk modeling
- Financial risk management
- R
- Mathematics
- Statistics
- Data science
- Machine learning title: ‘Probability Integral Transform: Theory and Applications’ —
Case Study: Application to Marketing Mix Modeling (MMM)
Overview of Marketing Mix Modeling
Introduction to MMM
Marketing Mix Modeling (MMM) is a statistical analysis technique used to estimate the impact of various marketing activities on sales and other key performance indicators. MMM helps businesses understand how different elements of the marketing mix—such as advertising, promotions, pricing, and distribution—affect consumer behavior and overall company performance.
Key components of MMM include:
- Data Collection: Gathering data from various sources, including sales data, marketing expenditure, economic indicators, and other external factors.
- Model Specification: Defining the relationship between marketing activities and outcomes using statistical models, typically regression-based.
- Parameter Estimation: Estimating the coefficients that quantify the impact of each marketing activity on sales.
- Validation and Refinement: Assessing the model’s accuracy and making necessary adjustments to improve its predictive power.
Importance in Marketing Science
Marketing Mix Modeling is crucial in marketing science for several reasons:
- Optimizing Marketing Spend: MMM provides insights into the return on investment (ROI) of different marketing activities, enabling companies to allocate their budgets more effectively.
- Strategic Decision Making: By understanding the relative effectiveness of various marketing tactics, businesses can make informed strategic decisions to enhance their market position.
- Forecasting and Planning: MMM helps in forecasting future sales based on planned marketing activities, assisting in better planning and resource allocation.
- Understanding Market Dynamics: It provides a deeper understanding of how different factors—both controllable (like pricing) and uncontrollable (like economic conditions)—influence consumer behavior.
- Measuring Campaign Effectiveness: MMM allows for the measurement of the effectiveness of specific marketing campaigns, helping to identify what works and what doesn’t.
Application of the Probability Integral Transform in MMM
Enhancing Model Fit Assessment
At our Labs, we have leveraged the Probability Integral Transform (PIT) to improve the accuracy of MMM model assessments. Here’s how we applied PIT to enhance the goodness of fit evaluation of our MMM models:
-
Transformation of Residuals: After estimating the MMM model, we applied the Probability Integral Transform to the residuals (the differences between observed and predicted values). This involved using the CDF of the residuals to transform them into a uniform distribution:
\[Y_i = F_{\epsilon}(\epsilon_i)\]where \(\epsilon_i\) are the residuals and \(F_{\epsilon}\) is the CDF of the residuals.
-
Uniformity Testing: By transforming the residuals, we converted them into a new variable that should be uniformly distributed if the model fits well. We then performed goodness of fit tests, such as the Kolmogorov-Smirnov test, to assess the uniformity of these transformed residuals.
-
Visual Diagnostics: We also used visual diagnostic tools, such as Q-Q plots, to compare the distribution of the transformed residuals to a uniform distribution. This helped in identifying any deviations from uniformity, indicating potential areas where the model might be improved.
-
Model Refinement: Based on the results of the goodness of fit tests and visual diagnostics, we refined our MMM models to better capture the underlying data patterns. This iterative process ensured that our models provided more accurate and reliable insights into the impact of marketing activities.
Benefits Realized
The application of the Probability Integral Transform in our MMM analysis at our Labs resulted in several key benefits:
- Increased Accuracy: The transformation allowed for a more precise assessment of model fit, leading to more accurate estimations of the impact of marketing activities.
- Better Validation: By converting residuals to a uniform distribution, we enhanced the reliability of our goodness of fit tests, providing stronger validation for our models.
- Improved Decision Making: The refined models offered more actionable insights, enabling better strategic and tactical decision making for our clients.
In conclusion, the Probability Integral Transform has proven to be a valuable tool in enhancing the robustness and accuracy of Marketing Mix Modeling. At our Labs, our innovative application of PIT has led to significant improvements in model validation and effectiveness, demonstrating its utility in advanced marketing analytics.
How PIT Improves MMM
Detailed Explanation of the Application
We have innovatively applied the Probability Integral Transform (PIT) to improve the robustness and accuracy of Marketing Mix Modeling (MMM). Here’s a detailed explanation of how PIT enhances MMM:
- Residual Analysis:
- Residuals: After fitting an MMM model, the residuals (the differences between the observed values and the values predicted by the model) are analyzed. The residuals should ideally be randomly distributed if the model is a good fit.
-
Transforming Residuals: We apply the Probability Integral Transform to the residuals. This involves using the cumulative distribution function (CDF) of the residuals to transform them into a new set of values that should follow a uniform distribution if the model fits well:
\[Y_i = F_{\epsilon}(\epsilon_i)\]Here, \(\epsilon_i\) are the residuals, and \(F_{\epsilon}\) is the CDF of the residuals.
- Assessing Uniformity:
- Uniformity Testing: After transforming the residuals, they should ideally follow a uniform distribution on the interval \([0, 1]\). We perform statistical tests such as the Kolmogorov-Smirnov test to compare the distribution of the transformed residuals against the uniform distribution. This helps in determining whether the residuals deviate from the expected uniformity, which would indicate a poor model fit.
- Visual Diagnostics: In addition to statistical tests, we use visual tools such as Q-Q (quantile-quantile) plots. By plotting the quantiles of the transformed residuals against the quantiles of a uniform distribution, we can visually inspect whether the residuals lie along a 45-degree line. Deviations from this line highlight areas where the model may need refinement.
- Iterative Model Refinement:
- Refinement Process: Based on the results of the uniformity tests and visual diagnostics, we iteratively refine the MMM model. This may involve adjusting the model structure, adding new variables, or transforming existing variables to better capture the underlying relationships.
- Validation: Each iteration involves reapplying the Probability Integral Transform and reassessing the uniformity of the transformed residuals. This iterative process continues until the residuals exhibit the desired uniform distribution, indicating a good model fit.
Benefits Realized Through the Use of the Transform
The application of the Probability Integral Transform in our MMM analysis has led to several significant benefits:
- Enhanced Accuracy:
- Precise Model Assessment: The transformation allows for a more precise assessment of the model’s goodness of fit. By converting the residuals to a uniform distribution, we can more accurately determine how well the model captures the data patterns.
- Reduction of Bias: Identifying and addressing deviations from uniformity helps in reducing model bias, leading to more reliable predictions and insights.
- Improved Model Validation:
- Robust Validation Framework: The use of PIT provides a robust framework for validating MMM models. The ability to transform residuals and test for uniformity enhances the credibility and reliability of the model validation process.
- Comprehensive Diagnostics: Combining statistical tests with visual diagnostics ensures that all aspects of model fit are thoroughly evaluated, leading to more robust model validation.
- Actionable Insights:
- Better Decision Making: More accurate and validated MMM models provide clearer and more actionable insights into the effectiveness of various marketing activities. This enables businesses to make informed strategic and tactical decisions, optimizing their marketing spend and improving overall performance.
- Identification of Improvement Areas: The iterative refinement process helps identify specific areas where the model can be improved, ensuring that the final model is finely tuned to the data and provides the most accurate insights possible.
- Efficiency in Analysis:
- Streamlined Process: The structured approach to applying PIT and iteratively refining the model streamlines the analysis process. This efficiency allows for quicker turnaround times in model development and validation, providing timely insights to stakeholders.
The application of the Probability Integral Transform has significantly enhanced the effectiveness of Marketing Mix Modeling. By enabling precise residual analysis and robust model validation, PIT has led to the development of highly accurate and actionable MMM models, driving better decision-making and improved marketing outcomes for our clients.
author_profile: false categories:
- Statistics classes: wide date: ‘2024-05-21’ excerpt: An in-depth guide to understanding and applying the Probability Integral Transform in various fields, from finance to statistics. header: image: /assets/images/data_science_2.jpg og_image: /assets/images/data_science_3.jpg overlay_image: /assets/images/data_science_2.jpg show_overlay_excerpt: false teaser: /assets/images/data_science_2.jpg twitter_image: /assets/images/data_science_3.jpg keywords:
- Probability integral transform
- Cumulative distribution function
- Goodness of fit
- Copula construction
- Financial risk management
- Monte carlo simulations
- Hypothesis testing
- Credit risk modeling
- R
- Mathematics
- Statistics
- Data science
- Machine learning seo_description: A comprehensive exploration of the probability integral transform, its theoretical foundations, and practical applications in fields such as risk management and marketing mix modeling. seo_title: ‘Probability Integral Transform: Theory and Applications’ seo_type: article summary: This article explains the Probability Integral Transform, its role in statistical modeling, and how it is applied in diverse fields like risk management, hypothesis testing, and Monte Carlo simulations. tags:
- Probability integral transform
- Cumulative distribution function
- Uniform distribution
- Copula construction
- Goodness of fit
- Monte carlo simulations
- Hypothesis testing
- Marketing mix modeling
- Credit risk modeling
- Financial risk management
- R
- Mathematics
- Statistics
- Data science
- Machine learning title: ‘Probability Integral Transform: Theory and Applications’ —
Appendix: Code Snippets in R
This appendix provides R code snippets demonstrating the application of the Probability Integral Transform in various contexts.
1. Inverse Transform Sampling
Inverse transform sampling is a method to generate random samples from any continuous distribution.
# Example: Generating random samples from an exponential distribution
set.seed(123) # For reproducibility
n <- 1000 # Number of samples
lambda <- 2 # Rate parameter for the exponential distribution
# Generate uniform random variables
u <- runif(n)
# Apply the inverse CDF (quantile function) of the exponential distribution
x <- -log(1 - u) / lambda
# Plot the histogram of the generated samples
hist(x, breaks = 50, main = "Exponential Distribution (lambda = 2)", xlab = "Value", col = "blue")
2. Applying the Probability Integral
Transforming data using the CDF of a distribution to check for uniformity.
# Example: Transforming normal residuals to check for uniformity
set.seed(123)
n <- 1000
mu <- 0
sigma <- 1
# Generate random samples from a normal distribution
x <- rnorm(n, mean = mu, sd = sigma)
# Calculate the CDF values of the samples
y <- pnorm(x, mean = mu, sd = sigma)
# Plot the histogram of the transformed data
hist(y, breaks = 50, main = "Uniform Distribution after PIT", xlab = "Value", col = "blue")
# Perform a Kolmogorov-Smirnov test to check uniformity
ks.test(y, "punif")
3. Goodness of Fit Test Using PIT
Using PIT to assess the goodness of fit of a model.
# Example: Goodness of fit test for a normal distribution
set.seed(123)
n <- 100
mu <- 0
sigma <- 1
# Generate random samples from a normal distribution
x <- rnorm(n, mean = mu, sd = sigma)
# Fit a normal distribution to the data
fit <- fitdistrplus::fitdist(x, "norm")
# Calculate the residuals
residuals <- (x - fit$estimate[1]) / fit$estimate[2]
# Apply the Probability Integral Transform
y <- pnorm(residuals)
# Plot Q-Q plot to check for uniformity
qqplot(qunif(ppoints(n)), y, main = "Q-Q Plot of Transformed Residuals")
abline(0, 1, col = "red")
# Perform a Kolmogorov-Smirnov test to check uniformity
ks.test(y, "punif")
4. Monte Carlo Simulation
Using the Probability Integral Transform in a Monte Carlo simulation to generate random samples from a specified distribution.
# Example: Monte Carlo simulation to estimate the value of π
set.seed(123)
n <- 10000
# Generate uniform random variables
u1 <- runif(n)
u2 <- runif(n)
# Check if points fall inside the unit circle
inside_circle <- (u1^2 + u2^2) <= 1
# Estimate π
pi_estimate <- (sum(inside_circle) / n) * 4
# Print the estimate
print(paste("Estimated value of π:", pi_estimate))
# Plot the points
plot(u1, u2, col = ifelse(inside_circle, "blue", "red"), asp = 1,
main = "Monte Carlo Simulation to Estimate π", xlab = "u1", ylab = "u2")
5. Generating Random Samples from a Custom Distribution
Generating samples from a custom distribution using the Probability Integral Transform.
# Example: Custom distribution defined by its CDF and inverse CDF
set.seed(123)
n <- 1000
# Define the inverse CDF (quantile function) for the custom distribution
custom_inv_cdf <- function(u) {
# Example: a simple piecewise linear function as a placeholder
ifelse(u < 0.5, u / 2, 1 - (1 - u) / 2)
}
# Generate uniform random variables
u <- runif(n)
# Apply the inverse CDF to generate samples from the custom distribution
x <- custom_inv_cdf(u)
# Plot the histogram of the generated samples
hist(x, breaks = 50, main = "Custom Distribution", xlab = "Value", col = "blue")



