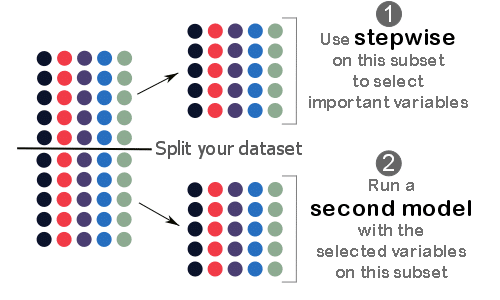
Stepwise Regression: Methodology, Applications, and Concerns

Stepwise Regression

Stepwise regression is a widely used technique in statistical modeling for selecting predictive variables. This method involves an automated procedure that iteratively adds or removes variables from a regression model based on predefined statistical criteria. The primary goal of stepwise regression is to identify a subset of variables that contribute most significantly to predicting the outcome variable, thereby optimizing the model’s fit.

The stepwise regression process can be particularly useful in situations where there are many potential explanatory variables and no clear theoretical guidance on which variables should be included in the model. By automating the variable selection process, stepwise regression provides a systematic approach to building a regression model that balances complexity and explanatory power.

There are three main approaches to stepwise regression: forward selection, backward elimination, and a combined approach. Forward selection starts with no variables and adds them one by one, while backward elimination starts with all candidate variables and removes them one by one. The combined approach alternates between adding and removing variables to find the best model fit.

Despite its popularity, stepwise regression has several limitations and potential pitfalls that practitioners should be aware of. One of the primary concerns is the risk of overfitting. Because stepwise regression explores a large number of possible models, it can lead to models that fit the training data very well but perform poorly on new, unseen data. This happens because the model may capture noise and idiosyncrasies specific to the training data rather than underlying patterns that generalize to other data sets.

Another significant issue is that the process of selecting variables step-by-step does not account for the uncertainty introduced by this selection. When the final model is chosen, the estimates and confidence intervals for the coefficients are often reported without adjustment for the selection process, leading to overly optimistic assessments of the model’s performance and reliability.

Furthermore, stepwise regression can sometimes produce misleading results, especially in cases where there is multicollinearity among the explanatory variables or where the sample size is small relative to the number of potential predictors. In extreme cases, stepwise regression can even identify statistically significant relationships in purely random data, underscoring the importance of validating the results with out-of-sample data or using alternative model selection techniques.

In light of these issues, it is crucial for practitioners to use stepwise regression judiciously and to be aware of its limitations. They should consider complementing stepwise regression with other model selection methods and employ robust validation techniques to ensure that the final model is both accurate and generalizable. Understanding the strengths and weaknesses of stepwise regression is essential for making informed decisions in statistical modeling and for drawing reliable conclusions from the data.

What is Stepwise Regression?

Stepwise regression is a method of fitting regression models that involves an automated process for selecting the most relevant predictive variables. This technique systematically evaluates each candidate variable and decides whether to include or exclude it from the model based on specific statistical criteria, such as p-values from t-tests or F-tests. The goal of stepwise regression is to build a parsimonious model that retains only the variables that contribute significantly to explaining the variability in the response variable.

The process of stepwise regression can be understood as an iterative sequence of steps where variables are added to or removed from the model. Each step is governed by predefined criteria, ensuring that the inclusion or exclusion of a variable is based on its statistical contribution to the model’s performance.

Key Steps in Stepwise Regression:

1. Initialization:
   • Forward Selection: The model starts with no variables. Variables are added one by one based on their statistical significance in improving the model fit.
   • Backward Elimination: The model starts with all potential variables. Variables are removed one by one based on their statistical insignificance in affecting the model fit.
   • Combined Approach: This method involves adding and removing variables in a stepwise manner, combining aspects of both forward selection and backward elimination.
2. Variable Addition (in Forward Selection):
   • At each step, the algorithm tests the addition of each candidate variable that is not yet in the model.
   • The variable that provides the most statistically significant improvement to the model fit is added.
   • The process repeats until no remaining variables offer a statistically significant improvement.
3. Variable Removal (in Backward Elimination):
   • At each step, the algorithm tests the removal of each variable currently included in the model.
   • The variable whose removal results in the least statistically significant deterioration of the model fit is excluded.
   • The process repeats until no further variables can be removed without significantly harming the model fit.
4. Model Refinement (in Combined Approach):
   • After adding a new variable, the algorithm checks whether any of the existing variables can be removed without significantly increasing the residual sum of squares (RSS).
   • This approach allows for a more dynamic model selection process, potentially leading to a better-fitting model.

Criteria for Variable Selection:

The decision to add or remove a variable is typically based on statistical tests such as:

• F-test: Used to compare models with and without a certain variable, assessing whether the variable significantly improves the model.
• t-test: Evaluates the significance of individual coefficients, determining if a variable’s contribution is statistically meaningful.

Advantages of Stepwise Regression:

• Automation: The process is automated, reducing the manual effort involved in variable selection.
• Model Simplification: Helps in identifying the most significant variables, leading to simpler and more interpretable models.
• Efficiency: Suitable for datasets with a large number of potential predictors, especially when there is no clear theoretical basis for selecting variables.

Limitations:

• Overfitting: The method can overfit the training data, especially if the number of candidate variables is large.
• Bias in Parameter Estimates: The final model’s estimates may be biased due to the stepwise selection process.
• Multicollinearity: The presence of multicollinearity among predictors can lead to unstable variable selection and coefficients.

In summary, stepwise regression is a valuable tool for model selection, providing a structured approach to identifying significant predictors. However, it is essential to be mindful of its limitations and to validate the final model rigorously to ensure its reliability and generalizability.

Approaches to Stepwise Regression

Stepwise regression employs various strategies for selecting the most relevant predictive variables in a regression model. The three primary approaches are forward selection, backward elimination, and a combined approach, each with distinct methodologies for adding or removing variables based on their statistical significance.

Forward Selection

Forward selection is an iterative process that begins with no variables in the model. The procedure involves the following steps:

1. Initial Model:
   • Start with an empty model containing no predictors.
2. Variable Addition:
   • Test each candidate variable for inclusion based on a chosen model fit criterion, such as the p-value from a t-test or the F-statistic.
   • Identify the variable that provides the most statistically significant improvement to the model fit.
   • Add this variable to the model.
3. Iteration:
   • Repeat the process, testing the remaining candidate variables for inclusion.
   • Continue adding variables until no additional variables significantly improve the model.

Forward selection is particularly useful when starting with a large set of potential predictors and there is no clear theoretical guidance on which variables should be included. It ensures that each added variable contributes meaningfully to the model’s explanatory power.

Backward Elimination

Backward elimination begins with a full model that includes all candidate variables. The procedure involves the following steps:

1. Initial Model:
   • Start with a model containing all potential predictors.
2. Variable Removal:
   • Test each variable for exclusion based on a chosen model fit criterion.
   • Identify the variable whose removal results in the least statistically significant deterioration of the model fit.
   • Remove this variable from the model.
3. Iteration:
   • Repeat the process, testing the remaining variables for exclusion.
   • Continue removing variables until no further variables can be eliminated without significantly harming the model’s performance.

Backward elimination is effective when starting with a comprehensive model and aiming to simplify it by removing non-significant predictors. This approach helps in refining the model to include only those variables that are essential for prediction.

Combined Approach

The combined approach, also known as stepwise selection, integrates elements of both forward selection and backward elimination. The procedure involves the following steps:

1. Initial Model:
   • Typically starts with no variables, similar to forward selection.
2. Variable Addition and Removal:
   • Add a new variable based on its statistical significance, as in forward selection.
   • After each addition, test the current set of variables to identify if any can be removed without significantly increasing the residual sum of squares (RSS).
   • Remove any non-significant variables identified in this step.
3. Iteration:
   • Continue adding and removing variables iteratively until no further variables can be added or removed based on the chosen criteria.

The combined approach allows for a more dynamic and flexible model selection process. It ensures that the model is not only progressively improved by adding significant variables but also continuously refined by removing redundant ones.

Each approach to stepwise regression—forward selection, backward elimination, and the combined approach—offers distinct advantages and is suitable for different modeling scenarios. Forward selection is ideal for building models from scratch, backward elimination for simplifying complex models, and the combined approach for a balanced and iterative refinement process. Understanding these methods allows practitioners to apply stepwise regression effectively while being mindful of potential pitfalls such as overfitting and multicollinearity.

Historical Context

The stepwise regression algorithm that is widely used today was first proposed by Efroymson in 1960. Efroymson’s method brought a significant advancement to the field of statistical modeling by introducing a systematic and automated approach to variable selection. This method is primarily a variation of forward selection, but with an important modification: at each stage of adding a new variable, the algorithm also checks if any of the previously included variables can be removed without significantly worsening the model’s performance.

Efroymson’s Algorithm

Efroymson’s algorithm operates by balancing the addition and removal of variables in a dynamic process. Here are the key steps and features of this algorithm:

1. Initialization:
   • The process begins with an empty model, containing no predictors.
2. Forward Selection:
   • Similar to standard forward selection, each potential predictor variable is tested for inclusion based on its ability to improve the model’s fit.
   • The variable that provides the most statistically significant improvement is added to the model.
3. Backward Elimination Check:
   • After adding a new variable, the algorithm examines all currently included variables to see if any can be removed without appreciably increasing the residual sum of squares (RSS).
   • This step ensures that the model remains as parsimonious as possible by eliminating any variables that do not contribute significantly to the explanatory power once new variables are added.
4. Iteration:
   • The process of adding and then potentially removing variables continues iteratively.
   • The algorithm terminates when adding additional variables does not result in a statistically significant improvement or when no more variables can be removed without a significant increase in RSS.

Impact and Usage

Efroymson’s algorithm has had a profound impact on statistical modeling and has been widely adopted in various fields, including economics, engineering, biomedical research, and social sciences. Its ability to handle numerous potential predictors and its systematic approach to variable selection make it a valuable tool in regression analysis.

However, it is important to recognize the limitations and potential pitfalls associated with stepwise regression, as discussed in previous sections. While Efroymson’s algorithm enhances the forward selection process by incorporating backward elimination checks, the fundamental issues of overfitting and bias in parameter estimates still apply. Practitioners should use this method judiciously and consider complementing it with other model selection techniques and robust validation methods.

Efroymson’s contribution to stepwise regression has provided a robust framework for automated model selection. By combining forward selection with backward elimination checks, his algorithm offers a more refined approach to building regression models. Understanding the historical context and mechanics of this algorithm helps practitioners appreciate its strengths and limitations, enabling them to apply it effectively in their statistical modeling endeavors.

Issues with Stepwise Regression

While stepwise regression is a popular method for model selection, it is not without significant drawbacks. Understanding these issues is crucial for practitioners to use the method effectively and avoid common pitfalls.

Overfitting

One of the primary concerns with stepwise regression is the risk of overfitting. The method searches through a large space of potential models, selecting the combination of variables that best fits the training data. This extensive search increases the likelihood of fitting not just the underlying signal but also the noise inherent in the data.

• Overfitting Explained: Overfitting occurs when a model captures the random fluctuations and idiosyncrasies of the training data rather than the true underlying patterns. As a result, the model performs exceptionally well on the training data but fails to generalize to new, unseen data, leading to poor predictive performance in practical applications.
• Mitigation Strategies: To mitigate overfitting, it is essential to use cross-validation techniques and holdout datasets to evaluate the model’s performance on out-of-sample data. Additionally, imposing penalties for model complexity, such as using information criteria (e.g., AIC or BIC), can help in selecting more parsimonious models.

Model Reporting and Inference

Another critical issue is the reporting of estimates and confidence intervals from the final selected model without adjusting for the model-building process.

• Misleading Inferences: When stepwise regression is used, the process of selecting variables introduces additional uncertainty. However, the standard practice often involves reporting the final model’s coefficients and their confidence intervals as if they were derived from a single, pre-specified model. This can lead to overconfidence in the estimates and potentially misleading inferences.
• Adjustments Needed: To address this, practitioners should account for the variable selection process when reporting results. Methods such as bootstrapping can be used to provide more accurate confidence intervals that reflect the uncertainty introduced by the selection process.

Misuse and Random Data

Stepwise regression can sometimes identify spurious relationships, particularly when dealing with random or highly correlated data.

• Spurious Results: There have been documented cases where stepwise regression has produced models with statistically significant predictors from random data. This highlights the method’s susceptibility to identifying false patterns, especially in datasets with many variables.
• Vigilance Required: To avoid falling into this trap, it is crucial to validate the selected model rigorously. This includes using out-of-sample validation, conducting sensitivity analyses, and ensuring that the identified relationships make theoretical and practical sense.

While stepwise regression offers a systematic approach to variable selection, it comes with significant risks and limitations. Practitioners must be vigilant about overfitting, accurately report the model’s uncertainty, and validate the model thoroughly to ensure its reliability. By understanding and addressing these issues, stepwise regression can be a valuable tool in the statistical modeling arsenal.

Conclusion

Stepwise regression is a powerful and widely used tool for model selection in statistical analysis. Its ability to systematically identify significant predictors from a large set of potential variables makes it appealing, especially in exploratory research and situations with many candidate predictors. However, this method comes with significant risks and limitations that practitioners must carefully consider.

Key Takeaways

• Risk of Overfitting: Stepwise regression can lead to overfitting by selecting a model that fits the training data too closely, capturing noise rather than the underlying signal. This results in a model that performs well on the training data but poorly on new, out-of-sample data.
• Uncertainty in Inference: The process of variable selection introduces additional uncertainty. Reporting estimates and confidence intervals from the final model without adjusting for this uncertainty can lead to misleading inferences.
• Potential for Spurious Results: The method’s tendency to explore a large model space increases the likelihood of identifying spurious relationships, particularly in datasets with many variables or when using random data.

Recommendations for Practitioners

• Use with Caution: While stepwise regression can be a valuable tool, it should be used judiciously and not as the sole method for model selection.
• Validate Models Rigorously: Employ robust validation techniques, such as cross-validation and the use of holdout datasets, to assess the model’s performance on out-of-sample data.
• Adjust for Model Selection: Consider methods that adjust for the model selection process when reporting results, such as bootstrapping, to provide more accurate estimates and confidence intervals.
• Consider Alternative Methods: Explore alternative model selection techniques, such as LASSO, ridge regression, or Bayesian model averaging, which can provide more stable and reliable results, especially in the presence of many predictors.

Final Thoughts

Understanding the strengths and weaknesses of stepwise regression is crucial for making informed decisions in statistical modeling. By being aware of its limitations and complementing it with rigorous validation and alternative methods, practitioners can leverage stepwise regression effectively while ensuring that the models they build are robust, reliable, and generalizable. Stepwise regression remains a valuable tool in the statistician’s toolkit, but its application must be accompanied by careful consideration and appropriate adjustments to mitigate its inherent risks.

References

• Efroymson, M. A. (1960). Algorithm for stepwise regression. In Ralston, A., & Wilf, H. S. (Eds.), Mathematical Methods for Digital Computers (pp. 191-203). Wiley.
• Draper, N. R., & Smith, H. (1998). Applied Regression Analysis (3rd ed.). Wiley-Interscience.
• Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction (2nd ed.). Springer.
• Harrell, F. E. (2015). Regression Modeling Strategies: With Applications to Linear Models, Logistic and Ordinal Regression, and Survival Analysis (2nd ed.). Springer.
• Derksen, S., & Keselman, H. J. (1992). Backward, Forward and Stepwise Automated Subset Selection Algorithms: Frequency of Obtaining Authentic and Noise Variables. British Journal of Mathematical and Statistical Psychology, 45(2), 265-282.
• Babyak, M. A. (2004). What You See May Not Be What You Get: A Brief, Nontechnical Introduction to Overfitting in Regression-Type Models. Psychosomatic Medicine, 66(3), 411-421.
• Steyerberg, E. W. (2009). Clinical Prediction Models: A Practical Approach to Development, Validation, and Updating. Springer.

Appendix A - Python Code

Here are some Python code examples that demonstrate the implementation of forward selection, backward elimination, and the combined approach for stepwise regression. We’ll use the statsmodels and scikit-learn libraries to facilitate these processes.

Setup

First, let’s import the necessary libraries and create a sample dataset.

import numpy as np
import pandas as pd
import statsmodels.api as sm
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

# Create a sample dataset
X, y = make_regression(n_samples=100, n_features=10, noise=0.1, random_state=42)
X = pd.DataFrame(X, columns=[f'X{i+1}' for i in range(X.shape[1])])
y = pd.Series(y, name='y')

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Forward Selection

def forward_selection(X, y):
    initial_features = []
    best_features = list(initial_features)
    remaining_features = list(X.columns)
    while remaining_features:
        scores_with_candidates = []
        for candidate in remaining_features:
            features = best_features + [candidate]
            X_train_new = sm.add_constant(X[features])
            model = sm.OLS(y, X_train_new).fit()
            score = model.aic
            scores_with_candidates.append((score, candidate))
        scores_with_candidates.sort()
        best_score, best_candidate = scores_with_candidates.pop(0)
        if len(best_features) == 0 or best_score < best_previous_score:
            best_features.append(best_candidate)
            best_previous_score = best_score
            remaining_features.remove(best_candidate)
        else:
            break
    return best_features

best_features = forward_selection(X_train, y_train)
print("Selected features:", best_features)

Backward Elimination

def backward_elimination(X, y):
    features = list(X.columns)
    while len(features) > 0:
        X_train_new = sm.add_constant(X[features])
        model = sm.OLS(y, X_train_new).fit()
        p_values = model.pvalues[1:]  # exclude the constant term
        max_p_value = p_values.max()
        if max_p_value > 0.05:
            excluded_feature = p_values.idxmax()
            features.remove(excluded_feature)
        else:
            break
    return features

selected_features = backward_elimination(X_train, y_train)
print("Selected features:", selected_features)

Combined Approach

def stepwise_selection(X, y):
    def fit_model(features):
        X_train_new = sm.add_constant(X[features])
        return sm.OLS(y, X_train_new).fit()

    initial_features = []
    best_features = list(initial_features)
    remaining_features = list(X.columns)
    while remaining_features:
        scores_with_candidates = []
        for candidate in remaining_features:
            features = best_features + [candidate]
            model = fit_model(features)
            score = model.aic
            scores_with_candidates.append((score, candidate))
        scores_with_candidates.sort()
        best_score, best_candidate = scores_with_candidates.pop(0)
        if len(best_features) == 0 or best_score < best_previous_score:
            best_features.append(best_candidate)
            best_previous_score = best_score
            remaining_features.remove(best_candidate)
            # After adding, check if any current features can be removed
            for feature in best_features[:-1]:
                features = list(best_features)
                features.remove(feature)
                model = fit_model(features)
                score = model.aic
                if score < best_previous_score:
                    best_features.remove(feature)
                    best_previous_score = score
        else:
            break
    return best_features

selected_features = stepwise_selection(X_train, y_train)
print("Selected features:", selected_features)

Testing the Final Model

Finally, we can train the final model using the selected features and evaluate its performance on the test set.

# Train the final model with the selected features
final_model = LinearRegression()
final_model.fit(X_train[selected_features], y_train)

# Evaluate the model on the test set
y_pred = final_model.predict(X_test[selected_features])
test_score = final_model.score(X_test[selected_features], y_test)
print("Test R^2 score:", test_score)

These code snippets demonstrate how to implement forward selection, backward elimination, and the combined approach for stepwise regression in Python. By selecting the most relevant features and training a linear regression model, we can evaluate the model’s performance on unseen data and assess its predictive power.

Appendix B - R Code

Here are the R code examples that demonstrate the implementation of forward selection, backward elimination, and the combined approach for stepwise regression. We’ll use the MASS and car libraries to facilitate these processes.

Setup

First, let’s create a sample dataset.

# Load necessary libraries
library(MASS)
library(car)

# Create a sample dataset
set.seed(42)
data <- as.data.frame(mvrnorm(100, mu = rep(0, 10), Sigma = diag(10)))
colnames(data) <- paste0("X", 1:10)
data$y <- with(data, 3*X1 + 2*X2 + rnorm(100))

# Split the data into training and testing sets
set.seed(42)
train_indices <- sample(1:nrow(data), 0.8 * nrow(data))
train_data <- data[train_indices, ]
test_data <- data[-train_indices, ]

Forward Selection

forward_selection <- function(train_data) {
  initial_model <- lm(y ~ 1, data = train_data)
  full_model <- lm(y ~ ., data = train_data)
  step(initial_model, scope = list(lower = initial_model, upper = full_model), direction = "forward")
}

forward_model <- forward_selection(train_data)
summary(forward_model)

Backward Elimination

backward_elimination <- function(train_data) {
  full_model <- lm(y ~ ., data = train_data)
  step(full_model, direction = "backward")
}

backward_model <- backward_elimination(train_data)
summary(backward_model)

Combined Approach

stepwise_selection <- function(train_data) {
  initial_model <- lm(y ~ 1, data = train_data)
  full_model <- lm(y ~ ., data = train_data)
  step(initial_model, scope = list(lower = initial_model, upper = full_model), direction = "both")
}

stepwise_model <- stepwise_selection(train_data)
summary(stepwise_model)

Testing the Final Model

Finally, we can train the final model using the selected features and evaluate its performance on the test set.

# Predict on the test set and evaluate the model
predict_test <- function(model, test_data) {
  predicted <- predict(model, newdata = test_data)
  actual <- test_data$y
  r_squared <- summary(lm(predicted ~ actual))$r.squared
  return(r_squared)
}

# Evaluate forward selection model
forward_r2 <- predict_test(forward_model, test_data)
cat("Forward Selection Test R^2:", forward_r2, "\n")

# Evaluate backward elimination model
backward_r2 <- predict_test(backward_model, test_data)
cat("Backward Elimination Test R^2:", backward_r2, "\n")

# Evaluate stepwise selection model
stepwise_r2 <- predict_test(stepwise_model, test_data)
cat("Stepwise Selection Test R^2:", stepwise_r2, "\n")

These R code examples illustrate how to implement forward selection, backward elimination, and a combined stepwise regression approach using the MASS and car libraries. Each method helps to select the most relevant features for building a regression model, but it’s essential to validate the final model to ensure its reliability and generalizability.

Appendix C - Julia Code

Below are the Julia code examples demonstrating the implementation of forward selection, backward elimination, and a combined approach for stepwise regression. We’ll use the GLM and DataFrames libraries to facilitate these processes.

Setup

First, let’s import the necessary packages and create a sample dataset.

using Random
using DataFrames
using GLM
using StatsBase

# Create a sample dataset
Random.seed!(42)
X = randn(100, 10)
y = 3 * X[:, 1] + 2 * X[:, 2] + randn(100)

data = hcat(DataFrame(X), y=y)
rename!(data, Symbol.(["X$i" for i in 1:10]) .=> ["X$i" for i in 1:10])

# Split the data into training and testing sets
train_indices = sample(1:size(data, 1), Int(0.8 * size(data, 1)), replace=false)
test_indices = setdiff(1:size(data, 1), train_indices)

train_data = data[train_indices, :]
test_data = data[test_indices, :]

Forward Selection

function forward_selection(train_data)
    initial_model = lm(@formula(y ~ 1), train_data)
    full_formula = @formula(y ~ X1 + X2 + X3 + X4 + X5 + X6 + X7 + X8 + X9 + X10)
    
    current_model = initial_model
    remaining_features = setdiff(terms(full_formula), terms(term(:y)), terms(current_model))
    best_features = []

    while !isempty(remaining_features)
        scores_with_candidates = []
        
        for candidate in remaining_features
            formula = @formula(y ~ $(join(best_features, "+")) + $(candidate))
            model = lm(formula, train_data)
            push!(scores_with_candidates, (aic(model), candidate))
        end
        
        scores_with_candidates = sort(scores_with_candidates, by=x->x[1])
        best_score, best_candidate = scores_with_candidates[1]

        push!(best_features, best_candidate)
        remaining_features = setdiff(remaining_features, best_candidate)
        current_model = lm(@formula(y ~ $(join(best_features, "+"))), train_data)
    end

    return current_model
end

forward_model = forward_selection(train_data)
print(summary(forward_model))

Backward Elimination

function backward_elimination(train_data)
    full_model = lm(@formula(y ~ X1 + X2 + X3 + X4 + X5 + X6 + X7 + X8 + X9 + X10), train_data)
    current_model = full_model
    current_features = terms(full_model)
    
    while length(current_features) > 1
        scores_with_candidates = []
        
        for candidate in current_features[2:end]  # Exclude the intercept term
            features = setdiff(current_features, candidate)
            formula = @formula(y ~ $(join(features, "+")))
            model = lm(formula, train_data)
            push!(scores_with_candidates, (aic(model), candidate))
        end
        
        scores_with_candidates = sort(scores_with_candidates, by=x->x[1])
        best_score, worst_candidate = scores_with_candidates[end]

        if aic(current_model) > best_score
            current_features = setdiff(current_features, worst_candidate)
            current_model = lm(@formula(y ~ $(join(current_features, "+"))), train_data)
        else
            break
        end
    end

    return current_model
end

backward_model = backward_elimination(train_data)
print(summary(backward_model))

Combined Approach

function stepwise_selection(train_data)
    initial_model = lm(@formula(y ~ 1), train_data)
    full_formula = @formula(y ~ X1 + X2 + X3 + X4 + X5 + X6 + X7 + X8 + X9 + X10)
    
    current_model = initial_model
    remaining_features = setdiff(terms(full_formula), terms(term(:y)), terms(current_model))
    best_features = []

    while !isempty(remaining_features)
        scores_with_candidates = []
        
        for candidate in remaining_features
            formula = @formula(y ~ $(join(best_features, "+")) + $(candidate))
            model = lm(formula, train_data)
            push!(scores_with_candidates, (aic(model), candidate))
        end
        
        scores_with_candidates = sort(scores_with_candidates, by=x->x[1])
        best_score, best_candidate = scores_with_candidates[1]

        push!(best_features, best_candidate)
        remaining_features = setdiff(remaining_features, best_candidate)
        current_model = lm(@formula(y ~ $(join(best_features, "+"))), train_data)
        
        # After adding, check if any current features can be removed
        for feature in best_features[1:end-1]
            features = setdiff(best_features, feature)
            formula = @formula(y ~ $(join(features, "+")))
            model = lm(formula, train_data)
            if aic(model) < best_score
                best_features = features
                best_score = aic(model)
            end
        end
    end

    return current_model
end

stepwise_model = stepwise_selection(train_data)
print(summary(stepwise_model))

Testing the Final Model

Finally, we can train the final model using the selected features and evaluate its performance on the test set.

# Predict on the test set and evaluate the model
function predict_test(model, test_data)
    predicted = predict(model, test_data)
    actual = test_data.y
    r_squared = 1 - sum((predicted - actual).^2) / sum((actual .- mean(actual)).^2)
    return r_squared
end

# Evaluate forward selection model
forward_r2 = predict_test(forward_model, test_data)
println("Forward Selection Test R²: ", forward_r2)

# Evaluate backward elimination model
backward_r2 = predict_test(backward_model, test_data)
println("Backward Elimination Test R²: ", backward_r2)

# Evaluate stepwise selection model
stepwise_r2 = predict_test(stepwise_model, test_data)
println("Stepwise Selection Test R²: ", stepwise_r2)

These Julia code examples illustrate how to implement forward selection, backward elimination, and a combined stepwise regression approach using the GLM and DataFrames libraries. Each method helps to select the most relevant features for building a regression model, but it’s essential to validate the final model to ensure its reliability and generalizability.

Check out Data Science Books on Amazon